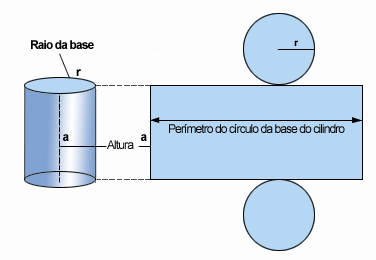
Planificações dos Sólidos Geométricos
Para se obter uma planificação é preciso verificar:
-
Se ela contem todas as figuras necessárias para sua composição;
-
Se as figuras estão presas uma a outra por, pelo menos, um lado nunca por uma ponta apenas;
-
Se o molde fecha, formando a figura desejada.

As formas que nos rodeiam
Os sólidos geométricos podem ser encontrados em diferentes formas que estão ao nosso redor, em nosso dia a dia. Uma caixa de sapatos, uma pirâmide, uma lata de óleo, um copo, uma casquinha de sorvete e muitas outras coisas, são consideradas sólidos geométricos.

Quantas coisas você conhece que tem essa forma?
Esse é o Prisma Quadrangular.
Quais das planificações da figura abaixo corresponde ao Prisma Quadrangular?
Existem dois tipos de sólidos geométricos: os poliedros e os não poliedros. São classificados como poliedros, todos os sólidos geométricos que possuem a superfície plana. Já os sólidos não poliedros são aqueles que possuem pelo menos uma superfície curva. Também conhecidos como Corpos Redondos.
São Corpos Redondos: A Esfera, o Cilindro e o Cone.
Planificações

Você sabe dizer de quais sólidos geométricos são essas planificações?
Pode existir mais de uma planificação para um mesmo sólido geométrico?
Outras formas de Prismas

Esta escrito "cuadrangular" por estar em castellano (espanhol).
A que sólido geométrico corresponde essa figura?
É um Poliedro Regular também conhecido como Sólido de Platão.
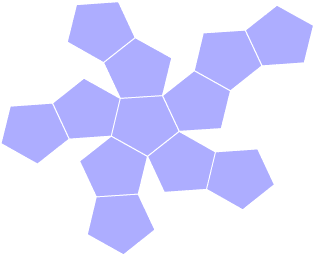
Quantas faces tem o Icosaedro?
Também é um Poliedro regular e também é um dos Sólidos de Platão

Para fazer em casa a Planificação do Cubo.
Ao recortar o papel, lembre de deixar as bordas (em branco na figura) para colar as faces.



Planificação do Prisma Pentagonal (observe as bordas para fazer a junção das faces)
Essa é a Planificação da Pirâmide de Base Quadrada.
E as figuras abaixo,
são as planificação de quais Sólidos Geométricos?





Poliedro regular
Sólido de Platão ...
Corpos Redondos - Planificações